How to Do You Know if a Piecewise Function is Continuous or Not

Let's consider a specific example of temperature in terms of date and location, such as June 27, 2013, in Phoenix, AZ. The graph in Figure 1 indicates that, at 2 a.m., the temperature was

${96}^{\circ }\text{F}$

. By 2 p.m. the temperature had risen to

${116}^{\circ }\text{F,}$

and by 4 p.m. it was

${118}^{\circ }\text{F}\text{.}$

Sometime between 2 a.m. and 4 p.m., the temperature outside must have been exactly

${110.5}^{\circ }\text{F}\text{.}$

In fact, any temperature between

${96}^{\circ }\text{F}$

and

${118}^{\circ }\text{F}$

occurred at some point that day. This means all real numbers in the output between

${96}^{\circ }\text{F}$

and

${118}^{\circ }\text{F}$

are generated at some point by the function according to the intermediate value theorem,

Look again at Figure 1. There are no breaks in the function's graph for this 24-hour period. At no point did the temperature cease to exist, nor was there a point at which the temperature jumped instantaneously by several degrees. A function that has no holes or breaks in its graph is known as a continuous function. Temperature as a function of time is an example of a continuous function.

If temperature represents a continuous function, what kind of function would not be continuous? Consider an example of dollars expressed as a function of hours of parking. Let's create the function

$D$

, where

$D\left(x\right)$

is the output representing cost in dollars for parking

$x$

number of hours.

Suppose a parking garage charges $4.00 per hour or fraction of an hour, with a $25 per day maximum charge. Park for two hours and five minutes and the charge is $12. Park an additional hour and the charge is $16. We can never be charged $13, $14, or $15. There are real numbers between 12 and 16 that the function never outputs. There are breaks in the function's graph for this 24-hour period, points at which the price of parking jumps instantaneously by several dollars.

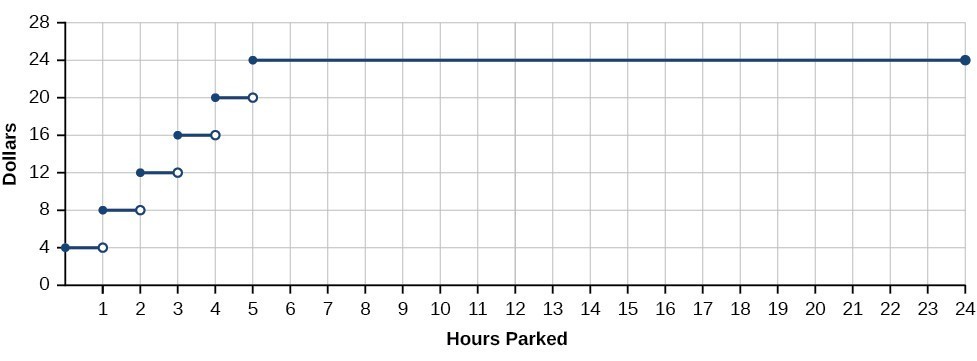Figure 2. Parking-garage charges form a discontinuous function.

A function that remains level for an interval and then jumps instantaneously to a higher value is called a stepwise function. This function is an example.

A function that has any hole or break in its graph is known as a discontinuous function. A stepwise function, such as parking-garage charges as a function of hours parked, is an example of a discontinuous function.

So how can we decide if a function is continuous at a particular number? We can check three different conditions. Let's use the function

$y=f\left(x\right)$

represented in Figure 3 as an example.

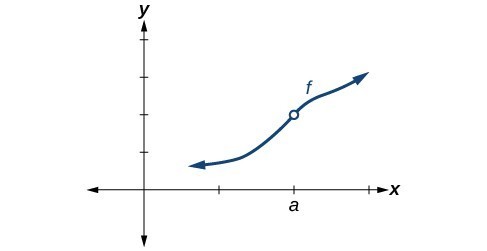Figure 3

Condition 1 According to Condition 1, the function

$f\left(a\right)$

defined at

$x=a$

must exist. In other words, there is a y-coordinate at

$x=a$

as in Figure 4.

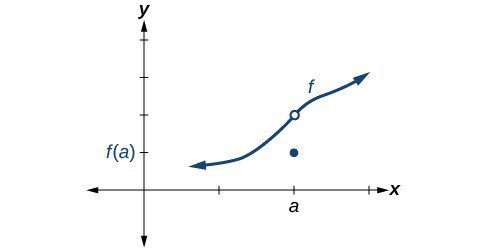Figure 4

Condition 2 According to Condition 2, at

$x=a$

the limit, written

$\underset{x\to a}{\mathrm{lim}}f\left(x\right)$

, must exist. This means that at

$x=a$

the left-hand limit must equal the right-hand limit. Notice as the graph of

$f$

in Figure 3 approaches

$x=a$

from the left and right, the same y-coordinate is approached. Therefore, Condition 2 is satisfied. However, there could still be a hole in the graph at

$x=a$

.

Condition 3 According to Condition 3, the corresponding

$y$

coordinate at

$x=a$

fills in the hole in the graph of

$f$

. This is written

$\underset{x\to a}{\mathrm{lim}}f\left(x\right)=f\left(a\right)$

.

Satisfying all three conditions means that the function is continuous. All three conditions are satisfied for the function represented in Figure 5 so the function is continuous as

$x=a$

.

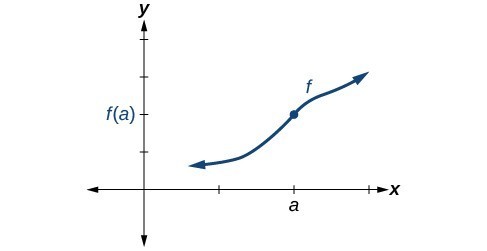Figure 5. All three conditions are satisfied. The function is continuous at

$x=a$

.

Figure 6 through Figure 9 provide several examples of graphs of functions that are not continuous at

$x=a$

and the condition or conditions that fail.

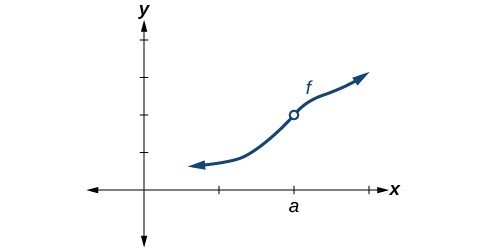Figure 6. Condition 2 is satisfied. Conditions 1 and 3 both fail.

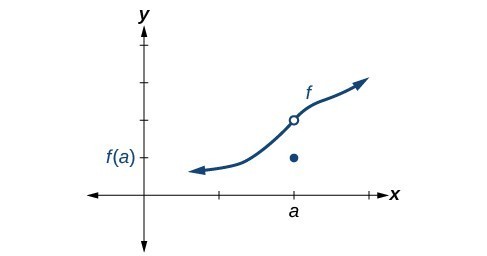Figure 7. Conditions 1 and 2 are both satisfied. Condition 3 fails.

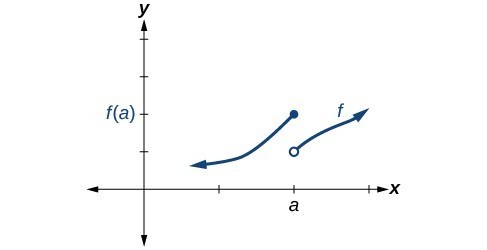Figure 8. Condition 1 is satisfied. Conditions 2 and 3 fail.

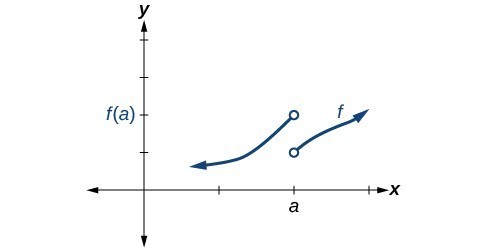Figure 9. Conditions 1, 2, and 3 all fail.

A General Note: Definition of Continuity

A function

$f\left(x\right)$

is continuous at

$x=a$

provided all three of the following conditions hold true:

Condition 1:

$f\left(a\right)$

exists.

Condition 2:

$\underset{x\to a}{\mathrm{lim}}f\left(x\right)$

exists at

$x=a$

.

Condition 3:

$\underset{x\to a}{\mathrm{lim}}f\left(x\right)=f\left(a\right)$

.

If a function

$f\left(x\right)$

is not continuous at

$x=a$

, the function is discontinuous at

$x=a$

.

Identifying Discontinuities

Discontinuity can occur in different ways. We saw in the previous section that a function could have a left-hand limit and a right-hand limit even if they are not equal. If the left- and right-hand limits exist but are different, the graph "jumps" at

$x=a$

. The function is said to have a jump discontinuity.

As an example, look at the graph of the function

$y=f\left(x\right)$

in Figure 10. Notice as

$x$

approaches

$a$

how the output approaches different values from the left and from the right.

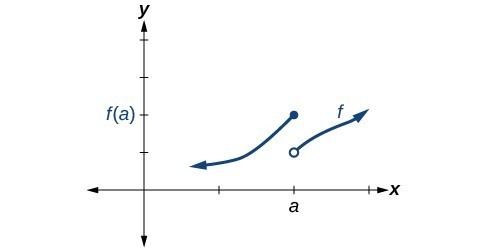Figure 10. Graph of a function with a jump discontinuity.

 A General Note: Jump Discontinuity

A function

$f\left(x\right)$

has a jump discontinuity at

$x=a$

if the left- and right-hand limits both exist but are not equal:

$\underset{x\to {a}^{-}}{\mathrm{lim}}f\left(x\right)\ne \underset{x\to {a}^{+}}{\mathrm{lim}}f\left(x\right)$

.

Identifying Removable Discontinuity

Some functions have a discontinuity, but it is possible to redefine the function at that point to make it continuous. This type of function is said to have a removable discontinuity. Let's look at the function

$y=f\left(x\right)$

represented by the graph in Figure 11. The function has a limit. However, there is a hole at

$x=a$

. The hole can be filled by extending the domain to include the input

$x=a$

and defining the corresponding output of the function at that value as the limit of the function at

$x=a$

.

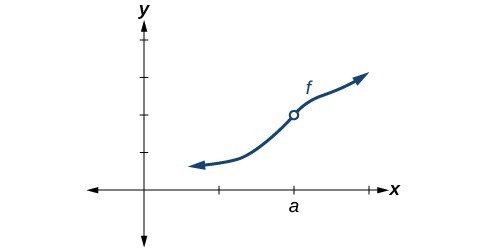Figure 11. Graph of function

$f$

with a removable discontinuity at

$x=a$

.

A General Note: Removable Discontinuity

A function

$f\left(x\right)$

has a removable discontinuity at

$x=a$

if the limit,

$\underset{x\to a}{\mathrm{lim}}f\left(x\right)$

, exists, but either

1. $f\left(a\right)$

   does not exist or

2. $f\left(a\right)$

   , the value of the function at

   $x=a$

   does not equal the limit,

   $f\left(a\right)\ne \underset{x\to a}{\mathrm{lim}}f\left(x\right)$

   .

Example 1: Identifying Discontinuities

Identify all discontinuities for the following functions as either a jump or a removable discontinuity.

1. $f\left(x\right)=\frac{{x}^{2}-2x - 15}{x - 5}$

2. $g\left(x\right)=\begin{cases}x+1, \qquad& x<2 \\ -x, \qquad& x\geq2\end{cases}$

Solution

1. Notice that the function is defined everywhere except at

   $x=5$

   .Thus,

   $f\left(5\right)$

   does not exist, Condition 2 is not satisfied. Since Condition 1 is satisfied, the limit as

   $x$

   approaches 5 is 8, and Condition 2 is not satisfied.This means there is a removable discontinuity at

   $x=5$

   .
2. Condition 2 is satisfied because

   $g\left(2\right)=-2$

   .Notice that the function is a piecewise function, and for each piece, the function is defined everywhere on its domain. Let's examine Condition 1 by determining the left- and right-hand limits as

   $x$

   approaches 2.Left-hand limit:

   $\underset{x\to {2}^{-}}{\mathrm{lim}}\left(x+1\right)=2+1=3$

   . The left-hand limit exists.Right-hand limit:

   $\underset{x\to {2}^{+}}{\mathrm{lim}}\left(-x\right)=-2$

   . The right-hand limit exists. But

   $\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)\ne \underset{x\to {2}^{+}}{\mathrm{lim}}f\left(x\right)$

   .

   So,

   $\underset{x\to 2}{\mathrm{lim}}f\left(x\right)$

   does not exist, and Condition 2 fails: There is no removable discontinuity. However, since both left- and right-hand limits exist but are not equal, the conditions are satisfied for a jump discontinuity at

   $x=2$

   .

Try It 1

Identify all discontinuities for the following functions as either a jump or a removable discontinuity.

a.

$f\left(x\right)=\frac{{x}^{2}-6x}{x - 6}$

b.

$g\left(x\right)=\begin{cases}\sqrt{x}, \qquad& 0\leq x<4 \\ 2x, \qquad& x\geq4\end{cases}$

Solution

Recognizing Continuous and Discontinuous Real-Number Functions

Many of the functions we have encountered in earlier chapters are continuous everywhere. They never have a hole in them, and they never jump from one value to the next. For all of these functions, the limit of

$f\left(x\right)$

as

$x$

approaches

$a$

is the same as the value of

$f\left(x\right)$

when

$x=a$

. So

$\underset{x\to a}{\mathrm{lim}}f\left(x\right)=f\left(a\right)$

. There are some functions that are continuous everywhere and some that are only continuous where they are defined on their domain because they are not defined for all real numbers.

A General Note: Examples of Continuous Functions

The following functions are continuous everywhere:

Polynomial functions	Ex: $f\left(x\right)={x}^{4}-9{x}^{2}$
Exponential functions	Ex: $f\left(x\right)={4}^{x+2}-5$
Sine functions	Ex: $f\left(x\right)=\sin \left(2x\right)-4$
Cosine functions	Ex: $f\left(x\right)=-\cos \left(x+\frac{\pi }{3}\right)$

The following functions are continuous everywhere they are defined on their domain:

Logarithmic functions	Ex: $f\left(x\right)=2\mathrm{ln}\left(x\right)$ , $x>0$
Tangent functions	Ex: $f\left(x\right)=\tan \left(x\right)+2$ , $x\ne \frac{\pi }{2}+k\pi$ , $k$ is an integer
Rational functions	Ex: $f\left(x\right)=\frac{{x}^{2}-25}{x - 7}$ , $x\ne 7$

How To: Given a function

$f\left(x\right)$

, determine if the function is continuous at

$x=a$

.

1. Check Condition 1:

   $f\left(a\right)$

   exists.
2. Check Condition 2:

   $\underset{x\to a}{\mathrm{lim}}f\left(x\right)$

   exists at

   $x=a$

   .
3. Check Condition 3:

   $\underset{x\to a}{\mathrm{lim}}f\left(x\right)=f\left(a\right)$

   .
4. If all three conditions are satisfied, the function is continuous at

   $x=a$

   . If any one of the conditions is not satisfied, the function is not continuous at

   $x=a$

   .

Example 2: Determining Whether a Piecewise Function is Continuous at a Given Number

Determine whether the function

$f\left(x\right)=\begin{cases}4x, \qquad& x\leq 3 \\ 8+x, \qquad& x>3\end{cases}$

is continuous at

1. $x=3$

2. $x=\frac{8}{3}$

Solution

To determine if the function

$f$

is continuous at

$x=a$

, we will determine if the three conditions of continuity are satisfied at

$x=a$

.

1. Condition 1: Does

   $f\left(a\right)$

   exist?

   $\begin{array}{l}f\left(3\right)=4\left(3\right)=12\qquad \\ \Rightarrow \text{Condition 1 is satisfied}.\qquad \end{array}$

   Condition 2: Does

   $\underset{x\to 3}{\mathrm{lim}}f\left(x\right)$

   exist?

   To the left of

   $x=3$

   ,

   $f\left(x\right)=4x$

   ; to the right of

   $x=3$

   ,

   $f\left(x\right)=8+x$

   . We need to evaluate the left- and right-hand limits as

   $x$

   approaches 1.

   Left-hand limit:

   $\underset{x\to {3}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {3}^{-}}{\mathrm{lim}}4\left(3\right)=12$

   Right-hand limit:

   $\underset{x\to {3}^{+}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {3}^{+}}{\mathrm{lim}}\left(8+x\right)=8+3=11$

Because

$\underset{x\to {1}^{-}}{\mathrm{lim}}f\left(x\right)\ne \underset{x\to {1}^{+}}{\mathrm{lim}}f\left(x\right)$

,

$\underset{x\to 1}{\mathrm{lim}}f\left(x\right)$

does not exist.

$\Rightarrow \text{ Condition 2 fails}\text{.}$

There is no need to proceed further. Condition 2 fails at

$x=3$

. If any of the conditions of continuity are not satisfied at

$x=3$

, the function

$f\left(x\right)$

is not continuous at

$x=3$

.

• $x=\frac{8}{3}$

  Condition 1: Does

  $f\left(\frac{8}{3}\right)$

  exist?

  $\begin{array}{l}f\left(\frac{8}{3}\right)=4\left(\frac{8}{3}\right)=\frac{32}{3}\qquad \\ \Rightarrow \text{Condition 1 is satisfied}.\qquad \end{array}$

  Condition 2: Does

  $\underset{x\to \frac{8}{3}}{\mathrm{lim}}f\left(x\right)$

  exist?

  To the left of

  $x=\frac{8}{3}$

  ,

  $f\left(x\right)=4x$

  ; to the right of

  $x=\frac{8}{3}$

  ,

  $f\left(x\right)=8+x$

  . We need to evaluate the left- and right-hand limits as

  $x$

  approaches

  $\frac{8}{3}$

  .

  Left-hand limit:

  $\underset{x\to {\frac{8}{3}}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {\frac{8}{3}}^{-}}{\mathrm{lim}}4\left(\frac{8}{3}\right)=\frac{32}{3}$

  Right-hand limit:

  $\underset{x\to {\frac{8}{3}}^{+}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {\frac{8}{3}}^{+}}{\mathrm{lim}}\left(8+x\right)=8+\frac{8}{3}=\frac{32}{3}$

  Because

  $\underset{x\to \frac{8}{3}}{\mathrm{lim}}f\left(x\right)$

  exists,

  $\Rightarrow \text{Condition 2 is satisfied}$

  .

  Condition 3: Is

  $f\left(\frac{8}{3}\right)=\underset{x\to \frac{8}{3}}{\mathrm{lim}}f\left(x\right)?$

  $\begin{array}{l}f\left(\frac{32}{3}\right)=\frac{32}{3}=\underset{x\to \frac{8}{3}}{\mathrm{lim}}f\left(x\right)\qquad \\ \Rightarrow \text{Condition 3 is satisfied}.\qquad \end{array}$

  Because all three conditions of continuity are satisfied at

  $x=\frac{8}{3}$

  , the function

  $f\left(x\right)$

  is continuous at

  $x=\frac{8}{3}$

  .

Try It 2

Determine whether the function

$f\left(x\right)=\begin{cases}\frac{1}{x}, \qquad& x\leq 2 \\ 9x-11.5, \qquad& x>2\end{cases}$

is continuous at

$x=2$

.

Solution

Example 3: Determining Whether a Rational Function is Continuous at a Given Number

Determine whether the function

$f\left(x\right)=\frac{{x}^{2}-25}{x - 5}$

is continuous at

$x=5$

.

Solution

To determine if the function

$f$

is continuous at

$x=5$

, we will determine if the three conditions of continuity are satisfied at

$x=5$

.

Condition 1:

$\begin{array}{l}f\left(5\right)\text{ does not exist}\text{.}\\ \Rightarrow \text{Condition 1 fails}.\end{array}$

There is no need to proceed further. Condition 2 fails at

$x=5$

. If any of the conditions of continuity are not satisfied at

$x=5$

, the function

$f$

is not continuous at

$x=5$

.

Analysis of the Solution

See Figure 12. Notice that for Condition 2 we have

$\begin{array}{l}\underset{x\to 5}{\mathrm{lim}}\frac{{x}^{2}-25}{x - 5}=\underset{x\to 3}{\mathrm{lim}}\frac{\overline{)\left(x - 5\right)}\left(x+5\right)}{\overline{)x - 5}}\qquad \\ \text{ }=\underset{x\to 5}{\mathrm{lim}}\left(x+5\right)\qquad \\ \text{ }=5+5=10\qquad \\ \text{ }\Rightarrow \text{Condition 2 is satisfied}.\qquad \end{array}$

At

$x=5$

, there exists a removable discontinuity.

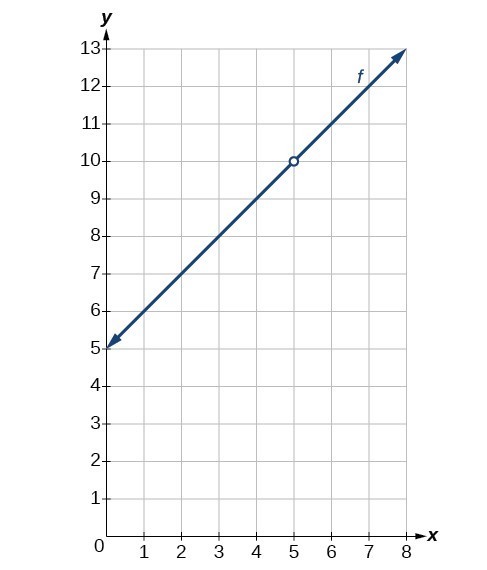Figure 12

Try It 3

Determine whether the function

$f\left(x\right)=\frac{9-{x}^{2}}{{x}^{2}-3x}$

is continuous at

$x=3$

. If not, state the type of discontinuity.

Solution

Determining the Input Values for Which a Function Is Discontinuous

Now that we can identify continuous functions, jump discontinuities, and removable discontinuities, we will look at more complex functions to find discontinuities. Here, we will analyze a piecewise function to determine if any real numbers exist where the function is not continuous. A piecewise function may have discontinuities at the boundary points of the function as well as within the functions that make it up.

To determine the real numbers for which a piecewise function composed of polynomial functions is not continuous, recall that polynomial functions themselves are continuous on the set of real numbers. Any discontinuity would be at the boundary points. So we need to explore the three conditions of continuity at the boundary points of the piecewise function.

How To: Given a piecewise function, determine whether it is continuous at the boundary points.

1. For each boundary point

   $a$

   of the piecewise function, determine the left- and right-hand limits as

   $x$

   approaches

   $a$

   , as well as the function value at

   $a$

   .
2. Check each condition for each value to determine if all three conditions are satisfied.
3. Determine whether each value satisfies condition 1:

   $f\left(a\right)$

   exists.
4. Determine whether each value satisfies condition 2:

   $\underset{x\to a}{\mathrm{lim}}f\left(x\right)$

   exists.
5. Determine whether each value satisfies condition 3:

   $\underset{x\to a}{\mathrm{lim}}f\left(x\right)=f\left(a\right)$

   .
6. If all three conditions are satisfied, the function is continuous at

   $x=a$

   . If any one of the conditions fails, the function is not continuous at

   $x=a$

   .

Example 4: Determining the Input Values for Which a Piecewise Function Is Discontinuous

Determine whether the function

$f$

is discontinuous for any real numbers.

$fx=\begin{cases}x+1, \qquad& x<2 \\ 3, \qquad& 2\leq x<4 \\ x^{2}-11, \qquad& x\geq 4\end{cases}$

Solution

The piecewise function is defined by three functions, which are all polynomial functions,

$f\left(x\right)=x+1$

on

$x<2$

,

$f\left(x\right)=3$

on

$2\le x<4$

, and

$f\left(x\right)={x}^{2}-5$

on

$x\ge 4$

. Polynomial functions are continuous everywhere. Any discontinuities would be at the boundary points,

$x=2$

and

$x=4$

.

At

$x=2$

, let us check the three conditions of continuity.

Condition 1:

$\begin{array}{l}f\left(2\right)=3\\ \Rightarrow \text{Condition 1 is satisfied}.\end{array}$

Condition 2: Because a different function defines the output left and right of

$x=2$

, does

$\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {2}^{+}}{\mathrm{lim}}f\left(x\right)?$

• Left-hand limit:

  $\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {2}^{-}}{\mathrm{lim}}\left(x+1\right)=2+1=3$

• Right-hand limit:

  $\underset{x\to {2}^{+}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {2}^{+}}{\mathrm{lim}}3=3$

Because

$3=3$

,

$\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {2}^{+}}{\mathrm{lim}}f\left(x\right)$

$\Rightarrow \text{Condition 2 is satisfied}$

.

Condition 3:

$\begin{array}{l}\underset{x\to 2}{\mathrm{lim}}f\left(x\right)=3=f\left(2\right)\\ \Rightarrow \text{Condition 3 is satisfied}.\end{array}$

Because all three conditions are satisfied at

$x=2$

, the function

$f\left(x\right)$

is continuous at

$x=2$

.

At

$x=4$

, let us check the three conditions of continuity.

Condition 2: Because a different function defines the output left and right of

$x=4$

, does

$\underset{x\to {4}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {4}^{+}}{\mathrm{lim}}f\left(x\right)?$

• Left-hand limit:

  $\underset{x\to {4}^{-}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {4}^{-}}{\mathrm{lim}}3=3$

• Right-hand limit:

  $\underset{x\to {4}^{+}}{\mathrm{lim}}f\left(x\right)=\underset{x\to {4}^{+}}{\mathrm{lim}}\left({x}^{2}-11\right)={4}^{2}-11=5$

Because

$3\ne 5$

,

$\underset{x\to {4}^{-}}{\mathrm{lim}}f\left(x\right)\ne \underset{x\to {4}^{+}}{\mathrm{lim}}f\left(x\right)$

, so

$\underset{x\to 4}{\mathrm{lim}}f\left(x\right)$

does not exist.

$\Rightarrow \text{Condition 2 fails}$

.

Because one of the three conditions does not hold at

$x=4$

, the function

$f\left(x\right)$

is discontinuous at

$x=4$

.

Analysis of the Solution

At

$x=4$

, there exists a jump discontinuity. Notice that the function is continuous at

$x=2$

.

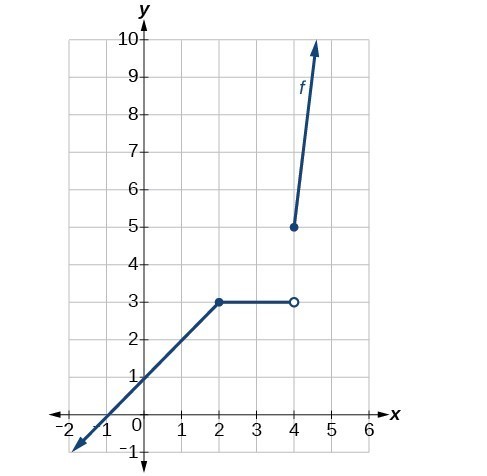Figure 13. Graph is continuous at

$x=2$

but shows a jump discontinuity at

$x=4$

.

Try It 4

Determine where the function

$f\left(x\right)=\begin{cases}\frac{\pi x}{4}, \qquad& x<2 \\ \frac{\pi}{x}, \qquad& 2\leq x \leq 6 \text{ is discontinuous.} \\ 2\pi x, \qquad& x>6\end{cases}$

Solution

Determining Whether a Function Is Continuous

To determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each of the functions that make up the piecewise function is continuous.

How To: Given a piecewise function, determine whether it is continuous.

1. Determine whether each component function of the piecewise function is continuous. If there are discontinuities, do they occur within the domain where that component function is applied?
2. For each boundary point

   $x=a$

   of the piecewise function, determine if each of the three conditions hold.

Example 5: Determining Whether a Piecewise Function Is Continuous

Determine whether the function below is continuous. If it is not, state the location and type of each discontinuity.

$fx=\begin{cases}sin\left(x\right), \qquad& x<0 \\ x^{3}, \qquad& x>0\end{cases}$

Solution

The two functions composing this piecewise function are

$f\left(x\right)=\sin \left(x\right)$

on

$x<0$

and

$f\left(x\right)={x}^{3}$

on

$x>0$

. The sine function and all polynomial functions are continuous everywhere. Any discontinuities would be at the boundary point,

At

$x=0$

, let us check the three conditions of continuity.

Condition 1:

$\begin{array}{l}f\left(0\right)\text{ does not exist}.\qquad \\ \Rightarrow \text{Condition 1 fails}.\qquad \end{array}$

Because all three conditions are not satisfied at

$x=0$

, the function

$f\left(x\right)$

is discontinuous at

$x=0$

.

Analysis of the Solution

There exists a removable discontinuity at

$x=0$

;

$\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=0$

, thus the limit exists and is finite, but

$f\left(a\right)$

does not exist.

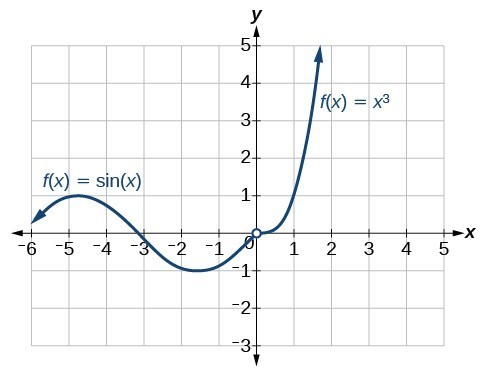Figure 14. Function has removable discontinuity at 0.

Key Concepts

• A continuous function can be represented by a graph without holes or breaks.
• A function whose graph has holes is a discontinuous function.
• A function is continuous at a particular number if three conditions are met:
  • Condition 1:

    $f\left(a\right)$

    exists.
  • Condition 2:

    $\underset{x\to a}{\mathrm{lim}}f\left(x\right)$

    exists at

    $x=a$

    .
  • Condition 3:

    $\underset{x\to a}{\mathrm{lim}}f\left(x\right)=f\left(a\right)$

    .
• A function has a jump discontinuity if the left- and right-hand limits are different, causing the graph to "jump."
• A function has a removable discontinuity if it can be redefined at its discontinuous point to make it continuous.
• Some functions, such as polynomial functions, are continuous everywhere. Other functions, such as logarithmic functions, are continuous on their domain.
• For a piecewise function to be continuous each piece must be continuous on its part of the domain and the function as a whole must be continuous at the boundaries.

Glossary

continuous function

a function that has no holes or breaks in its graph

discontinuous function

a function that is not continuous at

$x=a$

jump discontinuity

a point of discontinuity in a function

$f\left(x\right)$

at

$x=a$

where both the left and right-hand limits exist, but

$\underset{x\to {a}^{-}}{\mathrm{lim}}f\left(x\right)\ne \underset{x\to {a}^{+}}{\mathrm{lim}}f\left(x\right)$

removable discontinuity

a point of discontinuity in a function

$f\left(x\right)$

where the function is discontinuous, but can be redefined to make it continuous

Section Exercises

1. State in your own words what it means for a function

$f$

to be continuous at

$x=c$

.

2. State in your own words what it means for a function to be continuous on the interval

$\left(a,b\right)$

.

For the following exercises, determine why the function

$f$

is discontinuous at a given point

$a$

on the graph. State which condition fails.

3.

$f\left(x\right)=\mathrm{ln}\text{ }|\text{ }x+3\text{ }|,a=-3$

4.

$f\left(x\right)=\mathrm{ln}\text{ }|\text{ }5x - 2\text{ }|,a=\frac{2}{5}$

5.

$f\left(x\right)=\frac{{x}^{2}-16}{x+4},a=-4$

6.

$f\left(x\right)=\frac{{x}^{2}-16x}{x},a=0$

7.

$f\left(x\right)=\begin{cases}x,\qquad& x\neq 3 \\ 2x, \qquad& x=3\end{cases}a=3$

8.

$f\left(x\right)=\begin{cases}5, \qquad& x\neq 0 \\ 3, \qquad& x=0\end{cases} a=0$

9.

$f\left(x\right)=\begin{cases}\frac{1}{2-x}, \qquad& x\neq 2 \\ 3, \qquad& x=2\end{cases}a=2$

10.

$f\left(x\right)=\begin{cases}\frac{1}{x+6}, \qquad& x=-6 \\ x^{2}, \qquad& x\neq -6\end{cases}a=-6$

11.

$f\left(x\right)=\begin{cases}3+x, \qquad& x<1 \\ x, \qquad& x=1 \\ x^{2}, \qquad& x>1\end{cases}a=1$

12.

$f\left(x\right)=\begin{cases}3-x, \qquad& x<1 \\ x, \qquad& x=1 \\ 2x^{2}, \qquad& x>1\end{cases} a=1$

13.

$f\left(x\right)=\begin{cases}3+2x, \qquad& x<1 \\ x, \qquad& x=1 \\ -x^{2}, \qquad& x>1\end{cases}a=1$

14.

$f\left(x\right)=\begin{cases}x^{2}, \qquad& x<-2 \\ 2x+1, \qquad& x=-2 \\ x^{3}, \qquad& x>-2\end{cases}a=-2$

15.

$f\left(x\right)=\begin{cases}\frac{x^{2}-9}{x+3}, \qquad& x<-3 \\ x-9, \qquad& x=-3 \\ \frac{1}{x}, \qquad& x>-3\end{cases}a=-3$

16.

$f\left(x\right)=\begin{cases}\frac{x^{2}-9}{x+3}, \qquad& x<-3 \\ x-9, \qquad& x=-3 \\ -6, \qquad& x>-3\end{cases}a=3$

17.

$f\left(x\right)=\frac{{x}^{2}-4}{x - 2},\text{ }a=2$

18.

$f\left(x\right)=\frac{25-{x}^{2}}{{x}^{2}-10x+25},\text{ }a=5$

19.

$f\left(x\right)=\frac{{x}^{3}-9x}{{x}^{2}+11x+24},\text{ }a=-3$

20.

$f\left(x\right)=\frac{{x}^{3}-27}{{x}^{2}-3x},\text{ }a=3$

21.

$f\left(x\right)=\frac{x}{|x|},\text{ }a=0$

22.

$f\left(x\right)=\frac{2|x+2|}{x+2},\text{ }a=-2$

For the following exercises, determine whether or not the given function

$f$

is continuous everywhere. If it is continuous everywhere it is defined, state for what range it is continuous. If it is discontinuous, state where it is discontinuous.

23.

$f\left(x\right)={x}^{3}-2x - 15$

24.

$f\left(x\right)=\frac{{x}^{2}-2x - 15}{x - 5}$

25.

$f\left(x\right)=2\cdot {3}^{x+4}$

26.

$f\left(x\right)=\mathrm{-sin}\left(3x\right)$

27.

$f\left(x\right)=\frac{|x - 2|}{{x}^{2}-2x}$

28.

$f\left(x\right)=\tan \left(x\right)+2$

29.

$f\left(x\right)=2x+\frac{5}{x}$

30.

$f\left(x\right)={\mathrm{log}}_{2}\left(x\right)$

31.

$f\left(x\right)=\mathrm{ln}\text{ }{x}^{2}$

32.

$f\left(x\right)={e}^{2x}$

33.

$f\left(x\right)=\sqrt{x - 4}$

34.

$f\left(x\right)=\sec \left(x\right)-3$

.

35.

$f\left(x\right)={x}^{2}+\sin \left(x\right)$

36. Determine the values of

$b$

and

$c$

such that the following function is continuous on the entire real number line.

$f\left(x\right)=\begin{cases}x+1, \qquad& {1 }<{x }<{3 }\\ x^{2}+bx+c, \qquad& |x-2|\geq 1\end{cases}$

For the following exercises, refer to Figure 15. Each square represents one square unit. For each value of

$a$

, determine which of the three conditions of continuity are satisfied at

$x=a$

and which are not.

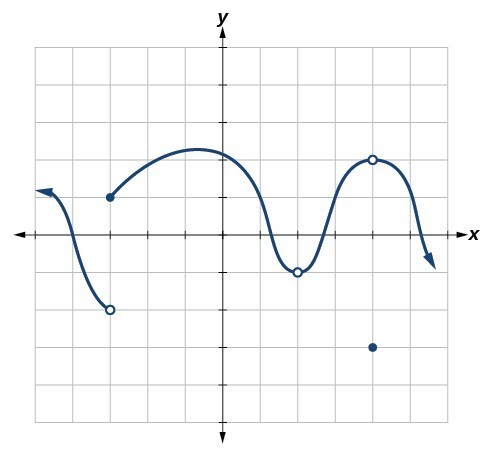Figure 15

37.

$x=-3$

38.

$x=2$

39.

$x=4$

For the following exercises, use a graphing utility to graph the function

$f\left(x\right)=\sin \left(\frac{12\pi }{x}\right)$

as in Figure 16. Set the x-axis a short distance before and after 0 to illustrate the point of discontinuity.

Figure 16

40. Which conditions for continuity fail at the point of discontinuity?

41. Evaluate

$f\left(0\right)$

.

42. Solve for

$x$

if

$f\left(x\right)=0$

.

43. What is the domain of

$f\left(x\right)?$

For the following exercises, consider the function shown in Figure 17.

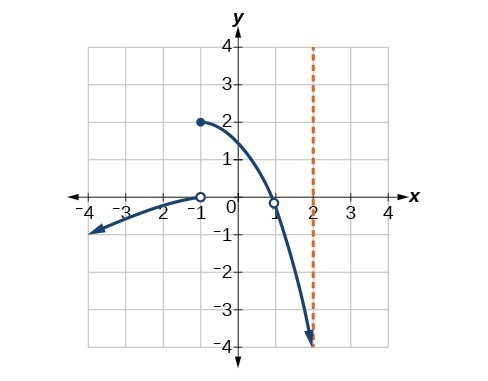Figure 17

44. At what x-coordinates is the function discontinuous?

45. What condition of continuity is violated at these points?

46. Consider the function shown in Figure 18. At what x-coordinates is the function discontinuous? What condition(s) of continuity were violated?

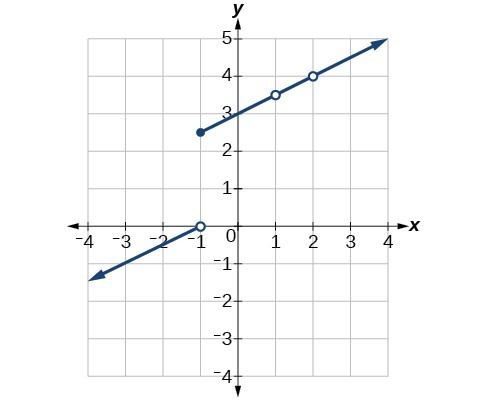Figure 18

47. Construct a function that passes through the origin with a constant slope of 1, with removable discontinuities at

$x=-7$

and

$x=1$

.

48. The function

$f\left(x\right)=\frac{{x}^{3}-1}{x - 1}$

is graphed in Figure 19. It appears to be continuous on the interval

$\left[-3,3\right]$

, but there is an x-value on that interval at which the function is discontinuous. Determine the value of

$x$

at which the function is discontinuous, and explain the pitfall of utilizing technology when considering continuity of a function by examining its graph.

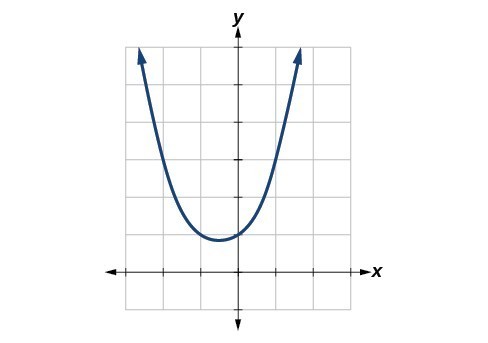Figure 19

49. Find the limit

$\underset{x\to 1}{\mathrm{lim}}f\left(x\right)$

and determine if the following function is continuous at

$x=1:$

50. The function is discontinuous at

$x=1$

because the limit as

$x$

approaches 1 is 5 and

$f\left(1\right)=2$

.

51. The graph of

$f\left(x\right)=\frac{\sin \left(2x\right)}{x}$

is shown in Figure 20. Is the function

$f\left(x\right)$

continuous at

$x=0?$

Why or why not?

Figure 20

Licenses and Attributions

goldwasuch.blogspot.com

Source: https://www.coursehero.com/study-guides/precalctwo/continuity/

Share this post